MST124 Unit 4 - Trigonometry
1 Right-angled triangles
1.1 Radians and degrees
An unbroken piece of a circumference of a circle is called an arc. The angle at the centre is said to be subtended by the arc.
One radian is the angle subtended at the centre of a circle by an arc that has the same length as the radius.
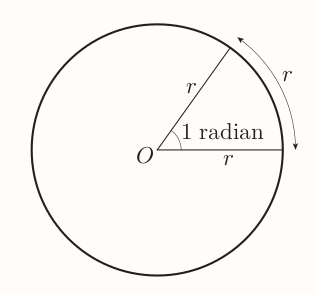
Given the circumference of a circle is $2\pi r$ and each arch of length $r$ subtends 1 radian then the number of radians in full circle is: $$ \frac{2\pi r}{r} = 2\pi = 360^{\circ} $$ This gives: $$ 1~\text{radian} = \frac{360^{\circ}}{2\pi} = \frac{180^{\circ}}{\pi} = 57.295... \approx 57^\circ $$
The number of radians in a fraction of full turn can be expressed in terms of $\pi$, e.g. $120^{\circ}= 2\pi/3$, $30^{\circ}= 2\pi/12 = \pi/6$, $90^\circ = \pi/2$...
Converting between degrees and radians
- number of radians $= \frac{\pi}{180} \times$ number of degrees
- number of degrees $= \frac{180}{\pi} \times$ number of radians
Length of an arc of a circle
$$ \text{arc length} = r\theta $$ where $r$ is the radius of the circle and $\theta$ is the angle subtended by the arc, measured in radians.
Area of a sector of a circle
$$ \text{area of sector} = \frac{1}{2}r^2\theta $$
1.2 Sine, cosine and tangent
$$ \begin{align} \sin\theta = \frac{\text{opp}}{\text{hyp}} \\[1em] \cos\theta = \frac{\text{adj}}{\text{hyp}} \\[1em] \tan\theta = \frac{\text{opp}}{\text{adj}} \\[1em] \end{align} $$
1.5 Trigonometric rations of special angles
Following special angles can be deduced without calculator:
- $\pi / 6 ~~ (30^{\circ})$
- $\pi / 4 ~~ (45^{\circ})$
- $\pi / 3 ~~ (60^{\circ})$
$\pi / 3$ is one of the angles of an equilateral triangle like:
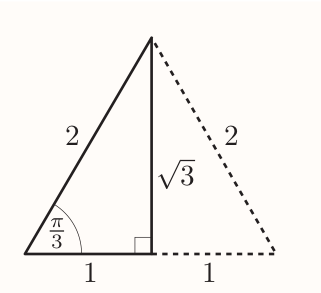
The lengths of the vertical line is: $$ \sqrt{2^2 - 1^2} = \sqrt{3} $$ Giving: $$ \sin\frac{\pi}{3} = \frac{\sqrt{3}}{2} ~~~ \cos\frac{\pi}{3} = \frac{1}{2} ~~~ \tan\frac{\pi}{3} = \frac{\sqrt{3}}{1} = \sqrt{3} $$
The ratio of $\pi/6$ can be found by using same diagram:
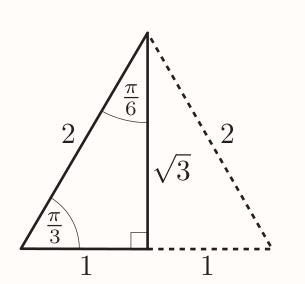
Giving: $$ \sin\frac{\pi}{6} = \frac{1}{2} ~~~ \cos\frac{\pi}{6} = \frac{\sqrt{3}}{2} ~~~ \tan\frac{\pi}{6} = \frac{1}{\sqrt{3}} $$
To find the ratios of $\pi/4$, following diagram can be used:
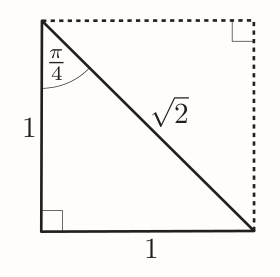
The length of the diagonal is: $$ \sqrt{1^2 + 1^2} = \sqrt{2} $$
Giving: $$ \sin\frac{\pi}{4} = \frac{1}{\sqrt{2}} ~~~ \cos\frac{\pi}{4} = \frac{1}{\sqrt{2}} ~~~ \tan\frac{\pi}{4} = \frac{1}{1} = 1 $$
Special angles table
| $\theta$ in radians | $\theta$ in degrees | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ |
|---|---|---|---|---|
| $\frac{\pi}{6}$ | $30^{\circ}$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{3}}$ |
| $\frac{\pi}{4}$ | $45^{\circ}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ | $1$ |
| $\frac{\pi}{3}$ | $60^{\circ}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | $\sqrt{3}$ |
It follows that e.g. $$ \cos^{-1}(\frac{\sqrt{3}}{2}) = \frac{\pi}{6} $$
It also follows that for any acute angle $\theta$, the value of $\sin\theta$ and $\cos\theta$ is less than 1.
1.6 Trigonometric identities
To find first two identities consider an acute angle $\theta$ in right-angled triangle such that
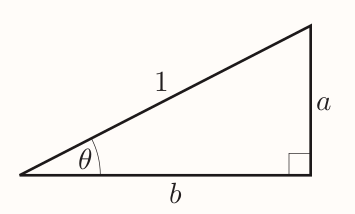
For which
$$
\sin\theta = \frac{a}{1} = a , \cos\theta = \frac{b}{1} = b , \tan\theta = \frac{a}{b}
$$
It follows that $$ \frac{\sin\theta}{\cos\theta} = \frac{a}{b} = \tan\theta $$ Giving the first identity.
Second identity can be found by applying the Pythagora's theorem: $$ a^2 + b^2 = 1^2 = 1 $$ Hence it follows that $$ (\sin\theta)^2 + (\cos\theta)^2 = 1 $$ Giving the second identity.
For next two identities consider:
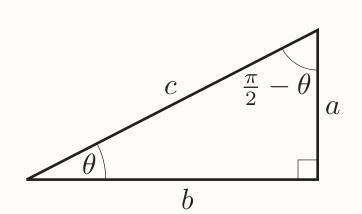
Where: $$ \sin\theta=\frac{a}{c} ~~ \cos\theta=\frac{b}{c} $$ Leading to next two identities: $$ \sin(\frac{\pi}{2} - \theta) = \frac{b}{c} = \cos\theta ~~ \cos(\frac{\pi}{2} - \theta) = \frac{a}{c} = \sin\theta $$
List of trigonometric identities
$$ \begin{align} \frac{\sin\theta}{\cos\theta} &= \tan\theta \\[1em] \sin^2\theta + \cos^2\theta &= 1 \\[1em] \sin(\frac{\pi}{2} - \theta) &= \cos\theta \\[1em] \cos(\frac{\pi}{2} - \theta) &= \sin\theta \\[1em] \end{align} $$
2 Trigonometric functions
2.1 Angles of any size
Besides acute and right angles we can have:
- obtuse angles (between $\pi/2$ and $\pi$)
- straight angles ($\pi$)
- reflex angles (between $\pi$ and $2\pi$)
There can also be angles larger than $2\pi$ or negative angles like $-\pi$.
The first step to find trigonometric rations of any angle is to associate a particular point $P$ with angle $\theta$ on the unit circle.
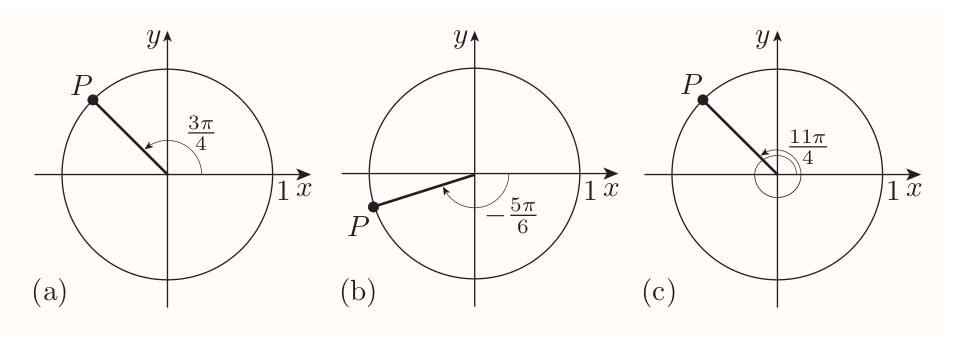
2.2 Sine, cosine and tangent of any angle
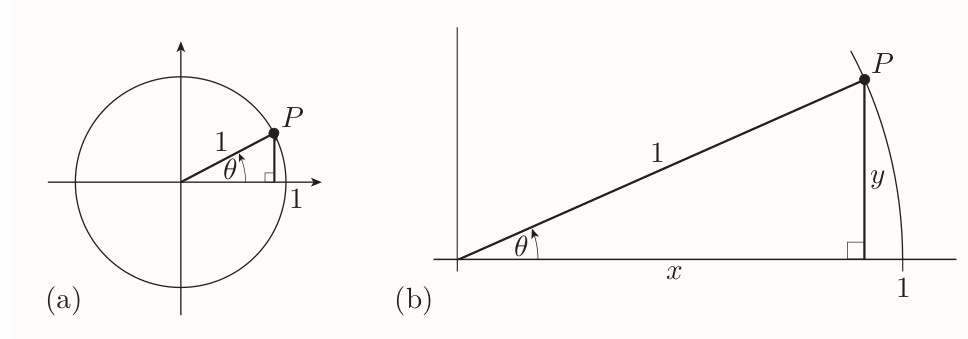
Sine, cosine and tangent
Suppose that $\theta$ is any angle and $(x, y)$ are the coordinates of its associated point $P$ on the unit circle. Then $$ \sin\theta = y~,~~ \cos\theta = x, \\ $$ and, provided that $x \ne 0$, $$ \tan\theta = \frac{y}{x} $$ (If $x = 0$, then $\tan\theta$ is undefined.)
ASTC diagram
Indicates which of the $\sin\theta$, $\cos\theta$ and $\tan\theta$ are positive.
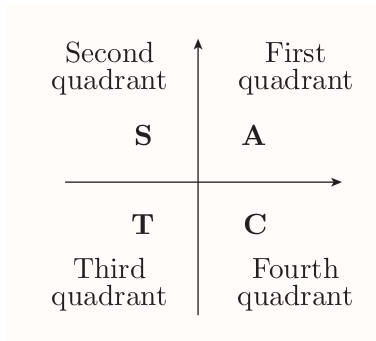
Suppose that $\theta$ is an angle whose associated point $P$ does not lie on either the $x$- or $y$-axis, and $\phi$ is the acute angle between $OP$ and the $x$-axis. Then $$ \begin{align} \sin\theta = \pm\sin\phi \\[0.5em] \cos\theta = \pm\cos\phi \\[0.5em] \tan\theta = \pm\tan\phi \\[0.5em] \end{align} $$ The ASTC diagram tells you which sign applies in each case. (The values $\sin\phi$, $\cos\phi$ and $\tan\phi$ are all positive, because $\phi$ is acute.)
2.3 Graphs of sine, cosine and tangent
Sine, cosine and tangent are trigonometric functions (rules with inputs and outputs).
The graph of the sine function
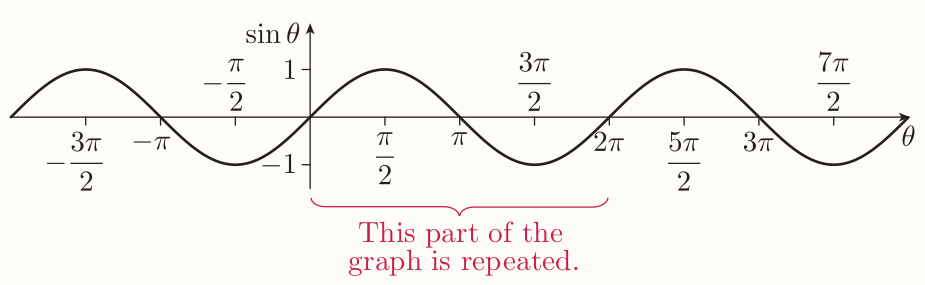
$\sin\theta$ is the $y$-coordinate of point $P$ on unit circle. As the angle $\theta$ increases from $0$ to $2\pi$, the point $P$ rotates from positive $x$-axis. Its $y$-coordinate oscillates from 0 to 1 to 0 to -1 and back to 0.
The graph oscillates endlessly since $\sin(\theta + 2\pi) = \sin\theta$ hence it's periodic with period $2\pi$.
The graph of the cosine function
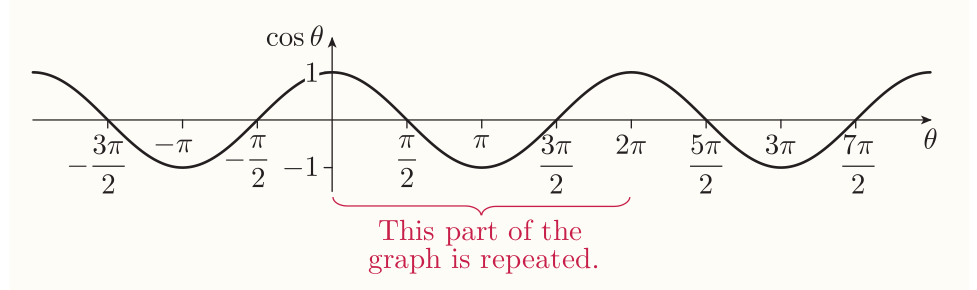
$\cos\theta$ is the $x$-coordinate of the point $P$ on the unit circle. It's periodic with period $2\pi$.
The graph of the tangent function
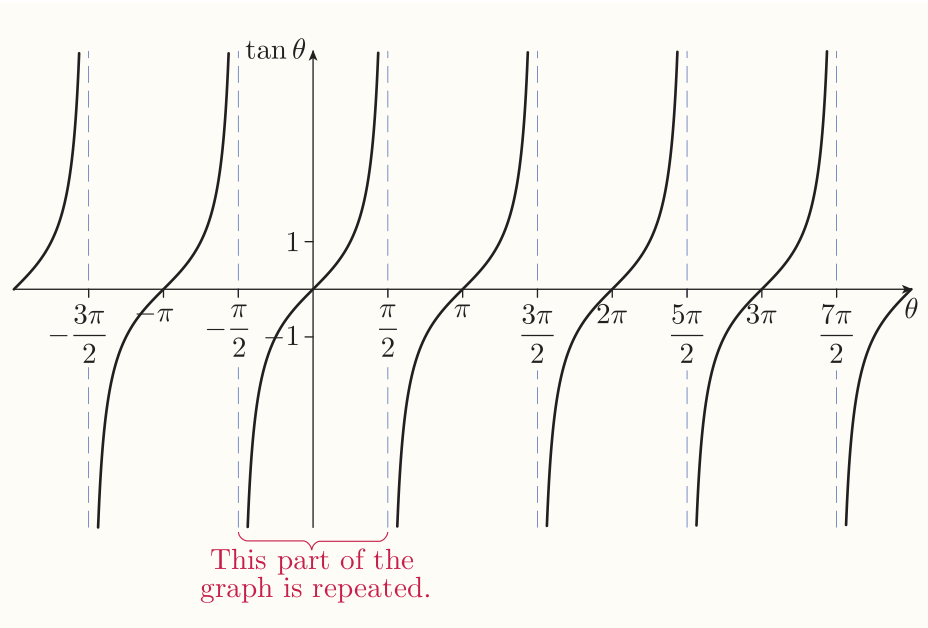
The graph is periodic with period of $\pi$. The breaks in graph occur when $\theta = \pi/2 + n\pi$ for some integer $n$. These are the values of $\theta$ for which $\tan\theta$ is undefined because the $x$-coordinate of the point $P$ is zero.
Using the variables $x$ and $y$ for trigonometric functions
Sometimes it's convenient to use the letter $x$ to denote the input variable and the letter $y$ to denote the output variable:
$$ y = \sin x ~~ y = \cos x ~~ y = \tan x $$
2.4 Inverse trigonometric functions
In general if a function $f$ is one-to-one, then it has an inverse function $f^{-1}$, whose rule is give by $$ f^{-1}(y) = x ~~~\text{where}~~~ f(x) = y $$ The sine, cosine and tangent aren't one-to-one, e.g.:
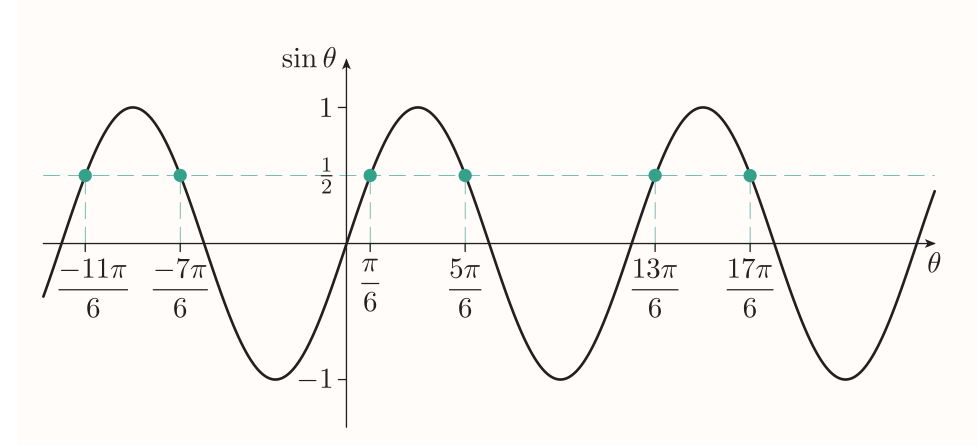
To obtain 'sort of inverse function' we need to specify new function with same rule but limited domain - a restriction:
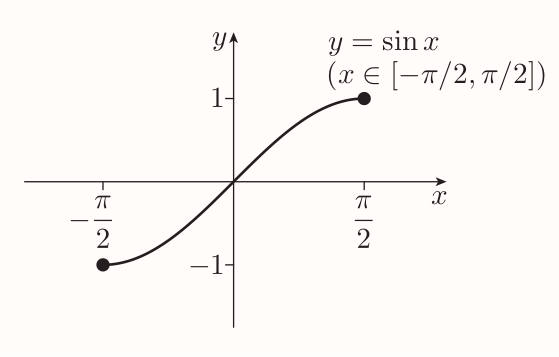
It has same image set as the sine function $[-1, 1]$ and it's increasing on the whole domain, so it's one-to-one. Hence it has an inverse function called the inverse sine function denoted by $\sin^{-1}$.
The graph of $y = \sin^{-1}(x)$ is reflection of $y = \sin(x)$ in the line $y = x$ (as with any other inverse function).
Inverse sine
The inverse sine function $\sin^{-1}$ is the function with domain $[-1, 1]$ and rule $$ \sin^{-1}x = y $$ where $y$ is the number in the interval $[-\pi/2, \pi/2]$ such that $\sin y=x$.
Inverse cosine
The inverse cosine function $\cos^{-1}$ is the function with domain $[-1, 1]$ and rule $$ \cos^{-1} x = y $$ where $y$ is the number in the interval $[0, \pi]$ such that $\cos y = x$
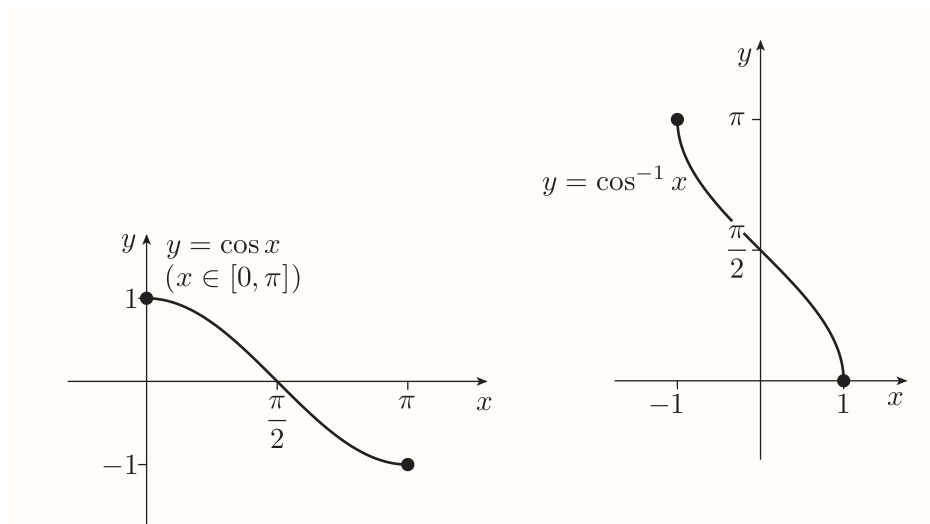
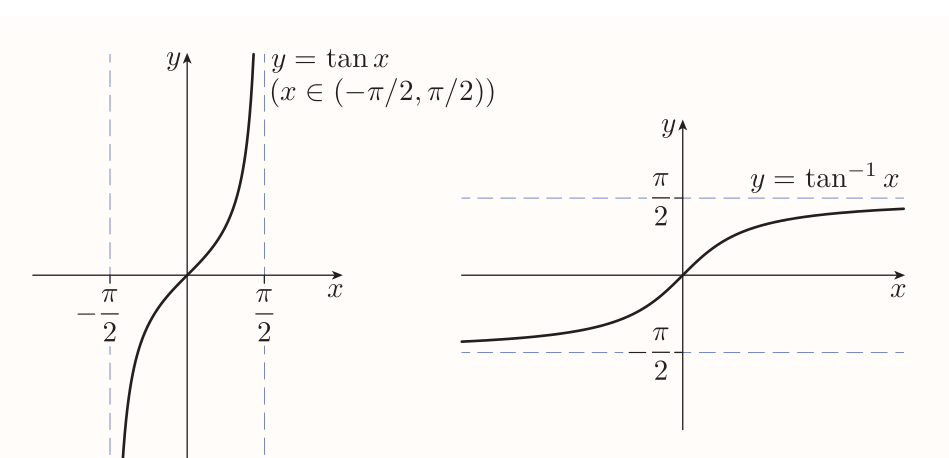
Inverse tangent
The inverse tangent function $\tan^{-1}$ is the function with domain $\mathbb{R}$ and rule $$ \tan^{-1} x = y $$ where $y$ is the number in the interval $(-\pi/2, \pi/2)$ such that $\tan y = x$.
Identities with negative inputs
$$ \begin{align} \sin^{-1}(-x) &= -\sin^{-1}x \\[0.4em] \cos^{-1}(-x) &= \pi -\cos^{-1}x \\[0.4em] \tan^{-1}(-x) &= -\tan^{-1}x \\[0.4em] \end{align} $$
2.5 Solving simple trigonometric equations
Like: $$ \sin\theta=\frac{1}{2},~~~\cos\theta=0.3,~~~\tan\theta=-1 $$ One solution can be found by applying an inverse trigonometric function: $$ \theta = \sin^{-1}\frac{1}{2} = \frac{\pi}{6} $$ However there are infinitely many other solutions since the sine is periodic. Hence it's the best to start by finding all the solutions in the interval of length $2\pi$, such as $[0, 2\pi]$ or $[-\pi, \pi]$ (there are usually two). Additional solutions ca be found by adding integer multiples of $2\pi$.
3 Sine and cosine rules
3.1 The sine rule
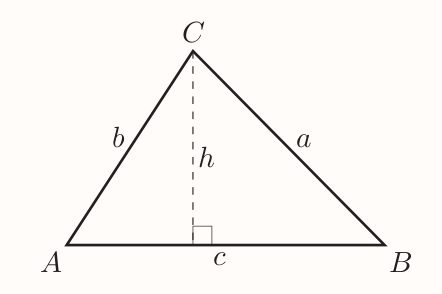
$$
\begin{align}
\sin A &= \frac{h}{b}, \text{so} h = b\sin A \\[0.4em]
\sin B &= \frac{h}{a}, \text{so} h = a\sin B \\[0.4em]
\text{hence} \\[0.4em]
b\sin A &= h = a \sin B \\[0.4em]
\frac{a}{\sin A} &= \frac{b}{\sin B}
\end{align}
$$
In same way, the line $h$ can be raised from other vertices and similar equation deduced.
Sine rule
$$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $$
Using the sine rule to find a side length
You can use the sine rule to find an unknown side length of a triangle if you know
- the opposite angle
- another side length and its opposite angle.
Using the sine rule to find an angle
You can use the sine rule to find an unknown angle in a triangle if you know:
- the opposite side length
- another side length and its opposite angle.
Sometimes you also need to know whether the unknown angle is acute or obtuse.
3.2 The cosine rule
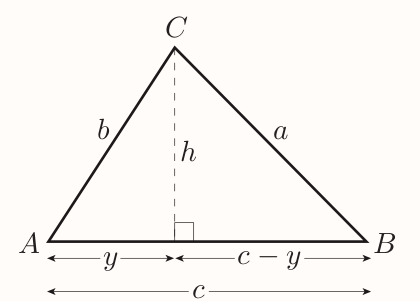
$$ \begin{align} b^2 &= y^2 + h^2 \\ a^2 &= (c - y)^2 + h^2 \\ \end{align} $$ Expanding the brackets in second term gives $$ a^2 = c^2 - 2cy + y^2 + h^2 $$ Since $y^2 + h^2 = b^2$ it follows that $$ a^2 = c^2 - 2cy + b^2 = b^2 + c^2 - 2cy $$ Next $$ \cos A = \frac{y}{b}, ~~\text{so} ~~ y = b\cos A $$ Substituting gives $$ a^2 = b^2 + c^2 - 2bc\cos A $$
Cosine rule
$$ \begin{align} a^2 = b^2 + c^2 - 2bc\cos A \\ b^2 = c^2 + a^2 - 2ca\cos B \\ c^2 = a^2 + b^2 - 2ab\cos C \\ \end{align} $$
Using the cosine rule to find a side length
You can use the cosine rule to find an unknown side length of a triangle if you know the other two side lengths and the angle between them.
Using the cosine rule to find an angle
You can use the cosine rule to find an unknown angle if you know all three side lengths.
Triangle solving tree
graph TD
l1(Does the triangle contain a right angle?)
l2a(Does the problem only involve lengths?)
l2b(Do you know a length and the angle opposite?)
l3a(Pythagoras' theorem)
l3b(Trigonometric ratios)
l3c(Sine rule)
l3d(Cosine rule)
l1 -- Y --> l2a
l1 -- N --> l2b
l2a -- Y --> l3a
l2a -- N --> l3b
l2b -- Y --> l3c
l2b -- N --> l3d
3.3 The area of triangle
For a triangle, $$ \text{area} = \frac{1}{2} \times \text{base} \times \text{height} $$
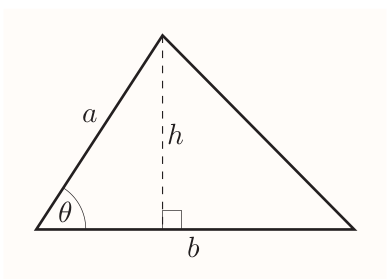
$$ \sin\theta = \frac{h}{a},~~~\text{so}~~ h = a\sin\theta $$ Hence
Area of triangle
For a triangle with an angle $\theta$ between two sides of lengths $a$ and $b$, $$ \text{area} = \frac{1}{2}ab\sin\theta $$
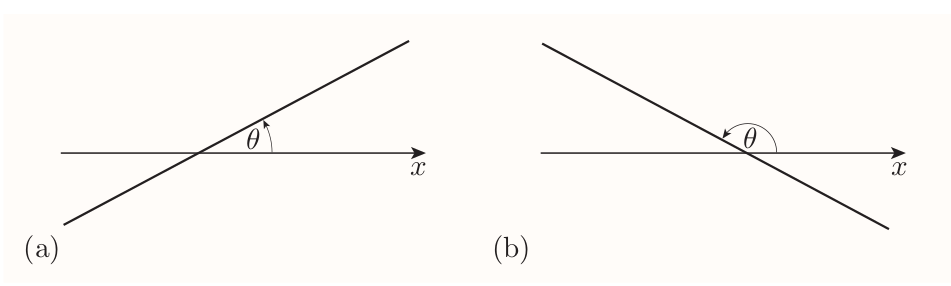
3.4 The angle of inclination of a line
is the angle that it makes with the $x$-axis, measured anticlockwise from the positive direction of the $x$-axis, when the line is drawn on axes with equal scales.
- a line with positive gradient has an angle of inclination between 0 and $\pi/2$
- a line with negative gradient has an angle of inclination between $\pi/2$ and $\pi$.
When a unit circle is considered:
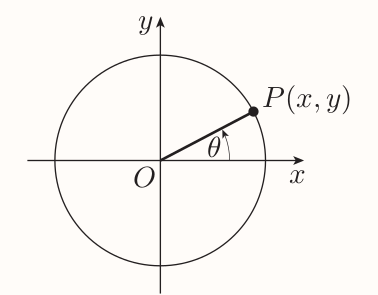
It's known that $$ \tan\theta = \frac{y}{x} $$ And by the formula for gradient $$ \text{gradient of OP} = \frac{y - 0}{x - 0} = \frac{y}{x} $$
hence
Gradient and angle of inclination of a straight line
For any non-vertical straight line with angle of inclination $\theta$, $$ \text{gradient} = \tan\theta $$ Remember that the angle of inclination is measured when the line is drawn on axes with equal scales.
4 Further trigonometric identities
4.1 Two simple trigonometric identities
First one is already known: $$ \tan\theta=\frac{\sin\theta}{\cos\theta} $$
Second can be deduced as follows:
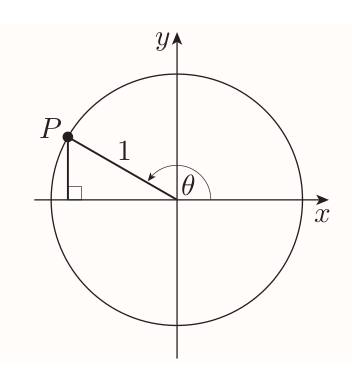
The length of the
- vertical side of triangle is $\sin\theta$.
- horizontal side of triangle is $-\cos\theta$
Hence by Pythagoras' theorem $$ \begin{align} (\sin\theta)^2 + (-\cos\theta)^2 = 1^2 \\ (\sin\theta)^2 + (\cos\theta)^2 = 1 \end{align} $$
Giving the second identity: $$ \sin^2\theta + \cos^2\theta = 1 $$
4.2 Trigonometric identities from the graphs of sine, cosine and tangent
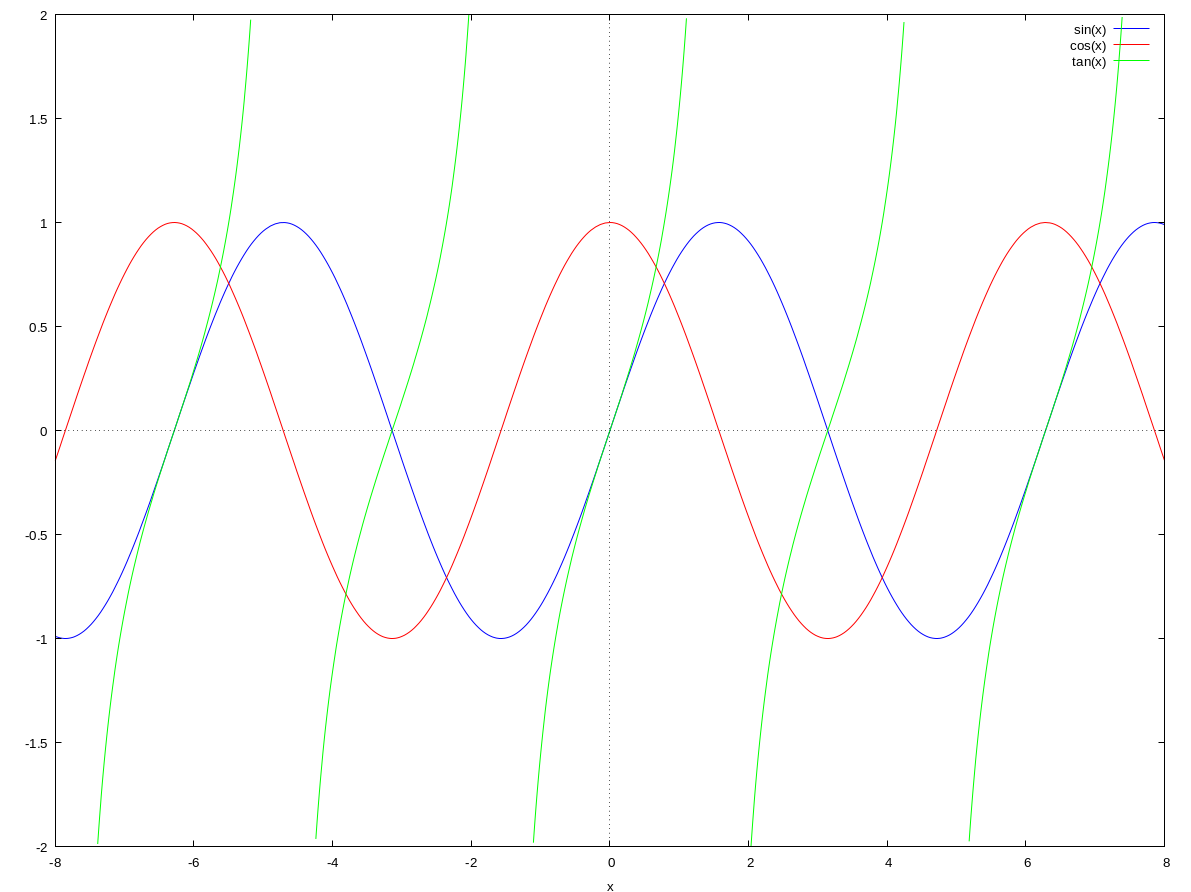
Given the trigonometric functions are periodic it follow that
$$ \begin{align} \sin(\theta + 2\pi) &= \sin\theta \\ \cos(\theta + 2\pi) &= \cos\theta \\ \tan(\theta + \pi) &= \tan\theta \\ \end{align} $$
From the symmetry of the respective graphs it also follows that $$ \begin{align} \sin(-\theta) &= -\sin\theta \\ \cos(-\theta) &= \cos\theta \\ \tan(-\theta) &= -\tan\theta \end{align} $$
Also, if the graph of cosine is translated to the left by $\pi/2$ and reflected in the vertical axis the graph of sine is obtained. Hence the equation $$ \cos(-\theta + \frac{\pi}{2}) = \sin\theta $$ is an identity. Similar identity can be found for since.
Hence following identities $$ \begin{align} \sin(\frac{\pi}{2} - \theta) = \cos\theta \\ \cos(-\theta + \frac{\pi}{2}) = \sin\theta \end{align} $$
4.3 Cosecant, secant and cotangent
In right angled triangle, three known trigonometric functions are defined as $$ \sin\theta = \frac{\text{opp}}{\text{hyp}} ~~~ \cos\theta = \frac{\text{adj}}{\text{hyp}} ~~~ \tan\theta = \frac{\text{opp}}{\text{adj}} ~~~ $$
There are three further ratios cosecant, secant, cotangent of $\theta$: $$ \text{cosec}\theta = \frac{\text{hyp}}{\text{opp}} ~~~ \text{sec}\theta = \frac{\text{hyp}}{\text{adj}} ~~~ \text{cot}\theta = \frac{\text{adj}}{\text{opp}} ~~~ $$
Generalized as
Cosecant, secant and cotangent
$$ \begin{align} \text{cosec}\theta &= \frac{1}{\sin\theta} ~~~(\text{provided} \sin\theta \ne 0) \\ \text{sec}\theta &= \frac{1}{\cos\theta} ~~~(\text{provided} \cos\theta \ne 0) \\ \text{cot}\theta &= \frac{\cos\theta}{\sin\theta} ~~~(\text{provided} \sin\theta \ne 0) \\ \end{align} $$
Given $$ \tan\theta = \frac{\sin\theta}{\cos\theta} $$
it follows that $$ \cot\theta = \frac{1}{\tan\theta} ~~~ (\text{provided} \sin\theta\ne0 ~\text{and} \cos\theta\ne0) $$
Essentially cosecant, secant and cotangent are the reciprocals of the sine, cosine and tangent functions (with same periods).
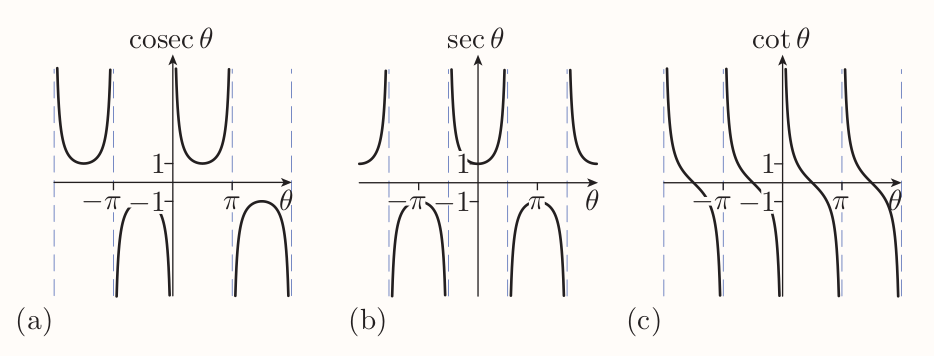
Two new identities can be obtained by taking previous identity $$ \sin^2\theta + \cos^2\theta = 1 $$ dividing both sides by $\cos^2\theta$ $$ \frac{\sin^2\theta}{\cos^2\theta} + \frac{\cos^2\theta}{\cos^2\theta} = \frac{1}{\cos^2\theta} $$ that is $$ \tan^2\theta + 1 = \sec^2\theta $$
Hence following identities $$ \begin{align} \tan^2\theta + 1 &= \sec^2\theta \\ 1 + \cot^2\theta &= \text{cosec}^2\theta \end{align} $$
4.4 Angle sum and angle difference identities
Angle sum identities for sine and cosine
$$ \begin{align} \sin(A + B) = \sin A \cos B + \cos A \sin B \\ \cos(A + B) = \cos A \cos B - \sin A \sin B \end{align} $$
Angle sum identity for tangent
$$ \tan(A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} $$
Angle difference identities
$$ \begin{align} \sin(A + B) = \sin A \cos B - \cos A \sin B \\ \cos(A - B) = \cos A \cos B + \sin A \sin B \\ \tan(A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \end{align} $$
4.5 Double-angle and half-angle identities
Double-angle identities
$$ \begin{align} \sin(2\theta) &= 2\sin\theta\cos\theta \\ \cos(2\theta) &= \cos^2\theta - sin^2\theta \\ \tan(2\theta) &= \frac{2\tan\theta}{1 - \tan^2\theta} \end{align} $$
Alternative double-angle identities for cosine
$$ \begin{align} \cos(2\theta) = 1 - 2\sin^2\theta \\ \cos(2\theta) = 2\cos^2\theta - 1 \end{align} $$
Half-angle identities
$$ \begin{align} \sin^2\theta = \frac{1}{2}(1 - \cos(2\theta)) \\ \cos^2\theta = \frac{1}{2}(1 + cos(2\theta)) \end{align} $$